Top-down Microarchitecture Analysis
Just as doing anything else complex in the world, performance engineering needs a good methodology to start with. A lot of time people have a spark in their mind “Oh it must be that {cache/IO/network/threading/anything} that my code is running slow” and head down immeidately into optimization, only to find out that it is not the bottleneck of the program in the end.
The TMA (Top-down Microarchitecture Analysis) is a good methodology proposed by Intel in 2014. It helps to identify ineffective usage of CPU microarchitecture of a program on a high level and could be used to establish a target direction for performance optimization.
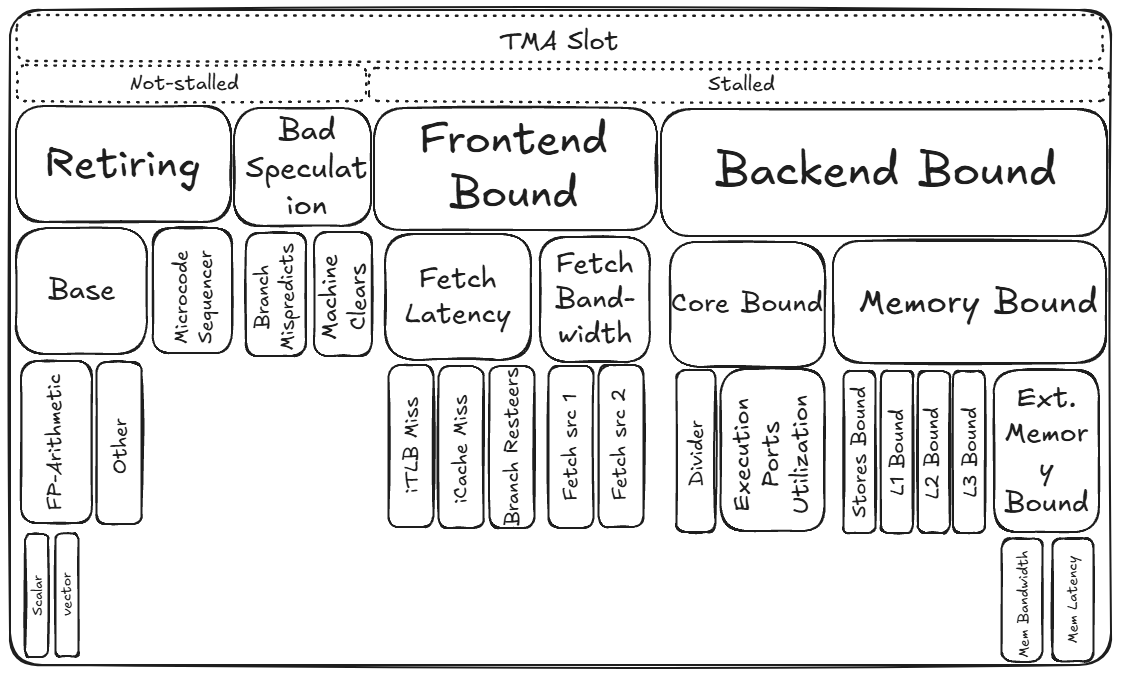
The above is a breakdown diagram of how TMA methodology analyze the execution of a program. Let’s walk through it step by step:
- Retiring: “Useful work”. Micro-ops execute and retire successfully.
- Base: Normal retired work from the regular decode/uop cache path
- FP-Arithmetic: retired instructions doing floating-point arthimetic
- Scalar: FP math using scalar instructions
- Vector: FP math using vectorized instructions (SSE/AVE)
- Other: non FP-Arithemtic instruction like integer ALU, load/store, control-flow, etc.
- FP-Arithmetic: retired instructions doing floating-point arthimetic
- Microcde Sequencer: Complex instructions (e.g. string ops) expanded by microcode into many internal uops; they retire but often with lower throughput.
- Base: Normal retired work from the regular decode/uop cache path
- Bad Speculation: Wasted work because speculation was wrong; uops execute but do no retire.
- Branch Mispredicts: Incorrect branch predications; work on the wrong is flushed.
- Machine Clears: Pipeline clears for non-branch reasons (memory-ordering violations, faults/traps, self-modifying code, etc.)
- Frontend Bound: The frontend (fetch/decode/uop cache) cannot supply uops fast enough.
- Fetch Latency: The frontend is waiting for instructions to arrive.
- iTLB Miss: Instruction-side TLB miss; page walk needed before fetch continues.
- iCache Miss: instruction cache miss (L1i). the frontend must fetch instructions from L2/L3/DRAM
- Branch Resteers: Frequent redirections of the fetch target (taken branches, returns, indirect jumps) create bubbles.
- Fetch Bandwidth: the frontend cannot deliver enough micro-ops per cycle to keep backend busy
- Fetch Latency: The frontend is waiting for instructions to arrive.
- Backend Bound: The backend cannot complete the instructions provided by the frontend fast enough.
- Core Bound: the backend is limited by execution resources and data-dependence scheduling
- Divider: Stalls from long-latency integer/FP divide units.
- Execution Port Utilization: Too many micro-ops competing for the same execution ports/units
- Memory Bound: the backend is waiting for data to perform operations upon
- Store Bound: Store-side bottlenecks (store buffer pressure, write combining, store-forwarding issues, commit bandwidth limits).
- L1 Bound: Delays at L1D (misses or structural conflicts)
- L2 Bound: Waiting for data from L2 (missed in L1)
- L3 Bound: Waiting for data from LLC (missed in L2)
- Exeternal Memory Bound: Data served from beyond the LLC-local DRAM, remote NUMA DRAM, or persistent storage
- Core Bound: the backend is limited by execution resources and data-dependence scheduling
By performing such a TMA on the program at hand, we would have a better direction on which part needs optimization and dig further.
A final word of caution, there is no substitute for reading the code and knowing what it is doing. Ultimately we need to pinpoint the exact lines that are not performant and work on it.